Gyroscope to roll, pitch and yaw
Now you know most practical things you need to know about accelerometers, we’ll continue with gyroscopes (other names: gyro, angular rate sensor).
A gyroscope is a very fancy name for a device that measures the angular rate (how much degrees per second it is rotating). The gyroscopes used in very critical applications (like a jumbo jet) are very advanced and complicated. Fortunately for us, there are some low-cost and small sized alternatives which are good enough. They are fabricated using MEMS (iMEMS) technology by big companies like Analog Devices.
Great! Let’s start with some theory:
As you probably remember from you physics class, position, velocity and acceleration are related to eachother: deriving the position, gives us velocity:
d x = v x
with x being the position on the x-axis and v x being the velocity along the x-axis.
Maybe less obvious, the same holds for angles. While velocity is the speed at which the position is changing, angular rate is nothing more than the speed the angle is changing. That’s right:
d alpha = angular rate = gyroscope output
with alpha being the angle. It’s starting to look pretty good! Knowing that the inverse of deriving (d .) is integrating (∫), we change our formula’s into:
∫ angular rate = ∫ gyroscope output = alpha
Woohoo, we found a relation between angle (attitude!) and our gyroscope’s output: integrating the gyroscope, gives us our attitude-angle.
Enough boring theory! Let’s take a look at some figures. The following figures all represent the same motion: I took a gyroscope, turned it 90 degrees left and back, and turned it 90 degrees right and back.
The raw data (used here) is what we get when we feed the gyroscope’s output (0-5 volt) into a 10-bit ADC (analog to digital convertor). So the raw values are between 0 and 1024. Here’s a figure of that:
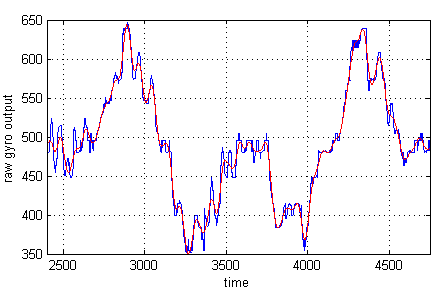
(The red line is just a low-pass filtered version of the blue data)
You can clearly see a positive angular rate followed by a negative one. But we’ll need to shift the figure down, to make sure negative values correspond to a negative angular rate. Otherwise the integration (which can be seen as the sum of our y-values) would keep adding up values and never substracting any! We normalize it by substracting about 490 from every value. This normalization gives us the following figure:
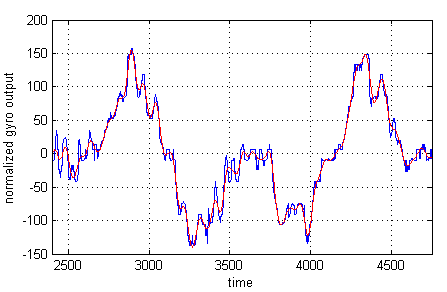
Now all we need to do, according to our formulas, is integrate it! Some of you may still have nightmares about college and start shivering when they hear the word integration, but its pretty simple. Discrete integration is nothing more than summing up all the values! Basically, integration from 0 to the i^th^ value:
integration(i) = integration (i-1) + vali
This is the simplest possible integrator. A more advanced one, which also flattens out possible jitter in the data, is the runge-kutta integrator:
integration(i) = integration(i-1) + 1⁄6 ( vali-3 + 2 vali-2 + 2 vali-1 + vali)
Using this runge-kutta integration, we get the following figure:
This is pretty much the exact movement I made! Now we just need to add a scale factor to our data so our result is in degrees:
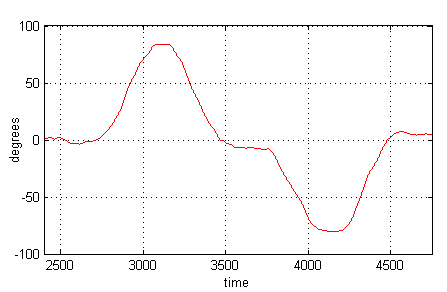
This pretty much ends my story of the simplified gyroscope!
In reality, gyroscopes are suffering from an effect called drift. This means that over time, the value a gyroscope has when in steady position (called bias), drifts away from it’s initial steady value:
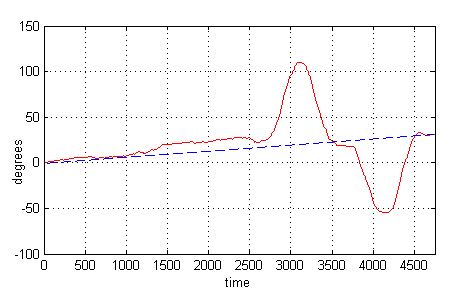
The blue line gives you an idea about the drift. During 4500 samples (12 seconds in my setup), the bias drifted about 30 degrees!
Remember that we need the bias (about 490 in our example) to normalize our data. How can we integrate when we have no idea about the currect bias? We’ll need to find a way to get it. More about this in the next article. A hint: our accelerometer isn’t affected by drift ;-)
|
hi
but still i am not able to understand that how can i get the values of Roll, pitch and yaw from the gyroscope data.
— vishal jain, 24 July 2006, 07:16 | #
Is the ‘drift’ just the quantization error you get when integrating a continuous signal in discrete chunks, or the result of some inherent quality of gyroscopes?
— Bergamot, 21 February 2007, 11:51 | #
I think it’s inherent to quality of gyroscopes, because if you use a runge kutta 4 the error is clearly negligible
— meno, 26 March 2007, 04:15 | #
drift is something typical for gyroscopes… the lighter/cheaper they are, the more drift (in general). The reason why you don’t see an error in the runge-kutta integrator, because the period is too small to notice it!
Runge-kutta just adds some low-pass filtering to eliminate the jitter
— Tom, 26 March 2007, 06:03 | #
Integrating pitch, roll, & yaw works for fixed wings but not helicopters. For copters U need to integrate a quaternion. Now how do you integrate gyro results into an attitude quaternion?
— x, 27 August 2007, 16:56 | #
Dear Sirs:
In this moment I am trying to build a C function to make the numerical integration of the ADXRS150 Gyro signal into the dsPIC30F processor.
In this way I want to implement a Runge-Kutta integration algorithm.
Can you advice me with some information, equation, paper or C examople code that help me to build it in my system?.
Thank you very much
Sincerely
Laura Andrea Gonzalez
— Laura Andrea Gonzalez, 27 October 2007, 17:19 | #
So, in an autopilot if we have both aceelerometers and gyros then which gives more precise results for calculating pitch, roll and yaw angles?
— Neha, 2 January 2008, 20:51 | #
Neha,
Normally a gyro (giving rotation in degrees per second) would, but because we have to integrate it to get the angle, the errors sum up over time. So we need another sensor to compensate the drift. Thats the accelerometer.
— Tom, 3 January 2008, 15:09 | #
One example of Inertial Measurement Unit (IMU) using two gyro (Analog Device), one accelerometer 3 axes (freescale) and a Microcontroller dsPIC from microchip :
http://www.kerhuel.eu/RTWdsPIC/examples/IMU.html
A complementary filter is implemented on the dsPIC using simulink.
— Lubin, 31 January 2008, 17:04 | #
continuous :“our accelerometer isn’t affected by drift” _
— khicon, 23 April 2008, 10:16 | #
Please, Can u advice me for an algorithm which can filter the noise of the gyro outputs
— Taher DERBEL, 24 May 2008, 09:43 | #
Hi, now i’m working with the adxrs300 rate sensor, also i’m working with the msp430f2619, but i have a problem, i take a first value of the gyro rate an then i substract this value to the actual adc value, so i can get positive and negative numbers for the integration, i’m using trapezoidal rule to integrate, but i get a lot of noise on the adc of the msp how could i solve this problem??.. Pls help me!!. i’m using batt to energize the gyro and microcontroller and some rc filters but still get noise, i i’m using the 3.3 v reference of the msp so i have to low the gyro out to 1.6 v at rest.
When i connect the batt the calculate angle stay for a moment in the mithe and then increase o decrease. it’s a little unstable and in 2 secs the bias is at 30 ° or more or less
— Sergio, 19 August 2008, 06:47 | #
The effect you notice is called gyro drift. The “neutral” value of your gyro starts drifting.
That why we need Kalman filtering in our data! It’s explained in the article http://tom.pycke.be/mav/71/kalman-filtering-of-imu-data
— Tom, 20 August 2008, 18:36 | #
hi Tom,
This blog is certainly perfect to understand flight motion, thanks for that. I calculate pitch and roll movement by gyro+accelerometer+kalman result is perfect.Additionally I want to calculate yaw motion.I know that i can not use accelerometer in there so i plan to design another thing like that gyro+magnetometer+kalman..Is it possible and how about efficiency.?Or have you any other idea about yaw movement detection..Thanks again..
— eakkas, 27 October 2008, 18:29 | #
eakkas, One thing im investigating is using optical flow to filter the gyro. The other way would be to use a compass?
— ehren, 30 November 2008, 04:11 | #
i want calculate pitch from rate Gyro
— eh, 8 December 2008, 08:25 | #
Hi Tom, thanks for your knowledge,
my question is: how to compensate the rectum uniformly accelerated motion on the accelerometer.
and your opinion on the use of Thermopile as horizon sensing
— Martin, 5 February 2009, 20:38 | #
hey dude,
what you do is not a runge-kutta integration algorithm, but rather a lowpass filtering of the simple integrated values… runge-kutta needs values between val_i and val_i-1 for an integration step size of T= t@val_i-t@vali_i-1 ! if you use runge kutta you have to take 3*T as the integration step time (time from val_i-3 to val_i)! if you do like described in your explanations you perform a runge-kutta with a time step= T and that’s wrong. this is not a runge-kutta, but rather a lowpass! i hope you know what i mean otherwise let me know!
— John, 18 April 2009, 11:21 | #
19. is the 10 bit adc sufficient for this measurement..
— ankit, 25 May 2009, 09:34 | #
Hi,
I need to develop an air mouse kind of remote. For that i need to use both accelerometer and gyro to derive x,y position. How can i use both of them effectively to derive x,y position??
— sony, 27 May 2009, 05:39 | #
Hi,Tom
Can you spit the shed the light on the issue that I use KF with accelero and gyro and in the air I have no respond to the angles,but when I turn the autopilot board with my hands I do have a respond.What is going on there?
— Paul, 21 June 2009, 15:28 | #
Hi Tom,
I am using IDG-1215. I tried to use the gyro output (which is converted to degree/s) to get the degree by multiplying it with a time elapsed. I kept turning my gyro. Below it is a protractor. I kept turning 20 degrees up and down in the yaw direction. I don’t really get the 20 degree. What is wrong actually? Can you please help?
— Miserable gyro user, 16 July 2009, 03:54 | #
Hi Tom,
Do you know of anyway accelerometer be used to measure yaw angle? I tried to implement that but the measurement is not accurate.
— Miserable gyro user, 17 July 2009, 10:25 | #
that drift we see, could it be due to “matemathical lag”? (i mean, since we need some values first to start integrating our position, the algorithm misses some part of the rotation…)
— Abraham Neddermann, 25 September 2009, 03:21 | #
Hi Tom, that i understand
bias = drift = initial value of gyroscope right?
i used analog device ADXRS300, drift = 2.5 volt right ?
if not could you please explain to me detail…
i am very confusing how to get it… thank you
— hard real time, 3 November 2009, 08:50 | #
HOLA!!! ME PODRIAS AYUDAR TENGO QUE HACER UN PROGRAMA EN MATLAB SOBRE EL METODO DEL RECTANGULO EN SUMAS INFERIORES PARA CALCULO INTEGRAL EN MATLAB, COMO LO HAGO?
— fernanda, 1 December 2009, 18:18 | #
Hi Tom could you please explain your runge kutta integration? i don’t understand.
— pizza, 26 January 2010, 04:51 | #