MAV-blog

This weekend I implemented a straightforward method for navigating around a circle. For the first day in like a 2 weeks, the weather was also nice enough to take my funjet for a testride. And yes, it worked quite well! I should check GPS logging to see how well in followed the circular path, but from the ground it looked fine.

How does it work

First we calculate which point on the circle we are currently closest to:
alpha = HeadingTowardsCircleCenter – PI

The closest point on the circle is the one at angle radians:
Lon = LonCircleCenter + sin( alpha ) * radius
Lat = LatCircleCenter + cos( alpha ) * radius

Of course we don’t need the point that is currently closest to us, but the one that is “within reasonable range”.
We calculate:
How much radians (circle radians) per second the UAV flies (if he would be on the circle):
(meter per second) / (radians per meter in circle)
vAngular = [radians per second] = UavSpeed / ( (2 * PI) / (2 * PI * radius) ) = UavSpeed / radius

Now comes the tricky part: we need to decide to which point on the circle we want to fly to. We calculate a new angle alpha2:
alpha2 = alpha + vAngular * tSeconds

We calculate the angle on the circle we should be at in tSeconds .

So we need to aim for the point on the circle tSeconds ahead of us:
Lon = LonCircleCenter + sin( alpha2 ) * radius
Lat = LatCircleCenter + cos( alpha2 ) * radius

How do we choose tSeconds? Good question. I quess it depends on how responsive your UAV is. I took 2 seconds on my first attempt. In the future I will experiment with other values.

Too far from the circle

One exception case should still be handled: What if we are too far from the circle? With the above algorithm, we would fly straight at the circle. This would be a huge problem because we might arrive at the circle with a heading that is perpendicular to the desired heading! In this case we could choose:
angle2 = angle + PI/2

The point at angle2 is the point on the circle where we would “touch” (and not cross) the circle if we were flying straight at it from a point far away from the circle. This is not optimal, because:
1. In most cases we are still quite close to the circle
2. In case of a big circle, we would not take the shortest route towards the circle
As a basic solution we can pick a smaller angle:
angle2 = angle + PI/4

Depending on the UAV’s agility, speed,current heading and distance from the circle, we could come up with a formula that yields an angle between 0 and PI/2. This still needs to be investigated. In a paper by Nathan D. Rasmussen, I found the following interesting yet visually trivial vector field for circle navigation:

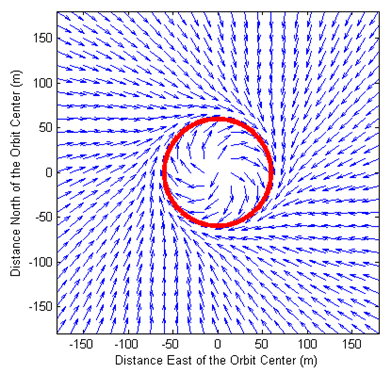
As a conclusion: complex solutions exist, but simple solutions work good enough in most cases!